2024华为杯detou4

0x00 前言

detours库的应用

有TLS反调试，不过不清楚怎么执行的

迷惑性很强

0x01 解

无壳，直接拖IDA

比较清晰，首先是一个key，key长为16Bytes，然后才是flag的输入

先解key，进去发现是这样的

v13[0] = 0x728C;
v13[1] = 0x5A38;
v13[2] = 0x767A;
v13[3] = 0x6AB9;
v13[4] = 0x6BAD;
v13[5] = 0x52D6;
v13[6] = 0x6ECF;
v13[7] = 0x68CF;
v13[8] = 0x5469;
v13[9] = 0x408B;
v13[10] = 0x58E3;
v13[11] = 0x4E1D;
v13[12] = 0x791F;
v13[13] = 0x5FC9;
v13[14] = 0x78F2;
v13[15] = 0x79CD;
v7 = operator new(0x48u);
v14 = 0;
if ( v7 )
  v2 = sub_D7135C(v7);
else
  v2 = 0;
v12 = v2;
strcpy(v11, "X:YsG:D4NL>ecG{8");
*(_WORD *)&v11[17] = 0;
v11[19] = 0;
v6 = operator new(0x48u);
v14 = 1;
if ( v6 )
  v3 = sub_D7135C(v6);
else
  v3 = 0;
v14 = -1;
v10 = v3;
sub_D71325(a1);
sub_D71325((int)v11);
v5 = operator new(0x48u);
v14 = 2;
if ( v5 )
  v4 = sub_D7135C(v5);
else
  v4 = 0;
v14 = -1;
sub_D71249(v12, v10);
for ( i = 0; i < 4; ++i )
{
  for ( j = 0; j < 4; ++j )
  {
    if ( v13[4 * i + j] != *(_DWORD *)(v4 + 16 * i + 8 + 4 * j) )
      return 0;
  }
}
return 1;

下面的sub_D71249是一个赋值，之后就是对比

for ( i = 0; ; ++i )
{
  result = this;
  if ( i >= *this )
    break;
  for ( j = 0; j < this[1]; ++j )
  {
    v7 = 0;
    for ( k = 0; k < *this; ++k )
      v7 += *(_DWORD *)(key + 16 * k + 8 + 4 * j) * *(_DWORD *)(insert + 16 * i + 8 + 4 * k);
    this[4 * i + 2 + j] = v7;
  }
}
return result;

看了一下是矩阵乘法$XA=B$，v13是B，v11那一串是A，所以要解只需要求$X=BA^{-1}$

import numpy as np
enc = [0x728C,0x5A38,0x767A,0x6AB9,0x6BAD,0x52D6,0x6ECF,0x68CF,0x5469,0x408B,0x58E3,0x4E1D,0x791F,0x5FC9,0x78F2,0x79CD]
key = [ord(x) for x in list('X:YsG:D4NL>ecG{8')]
B = np.array(enc).reshape(4,4)
A = np.array(key).reshape(4,4)
A_inv = np.linalg.inv(A)
X = np.dot(B, A_inv)
X = np.around(X).reshape(-1).astype(int).tolist()
for i in X:
    print(chr(i),end='')
# DBapaEHVB03UcXlM

继续向下看，发现flag长度为32Bytes，key和输入被丢进去做运算了

sub_D71217一直跟进去可以发现一个表

查询发现是SM4的加密

所以sub_D714A1就是生成轮密钥的

直接拿SM4解

好吧，看来没这么简单

上动调，一启动就退，应该是有反调试，通过查看导出表发现有TLS的存在

进去发现不知道用了什么反调试方法，根据题目名称detou4猜测用了detours库

一时半会找不出来反调试怎么做的（太菜了），直接上x96dbg用插件开反反调试过掉（挖坑，要过一遍所有反反调试方法）

因为发现连输入假flag判断都是错误的

所以定位比较函数sub_D710AF，从这里下手（由于是后面复现，所以需要先运行IDA得到新的地址然后去x96dbg定位）

进去会发现和原先的程序不同

中间被劫持了

跟进去发现同样也是调了对比函数，但是对比的内容被劫持改掉了

所以真正的密文在这

之后进到真正对比的函数

调试发现输入加密后的结果都不一样了

看来前面还有劫持，但是在哪这是个好问题

经过动调一步步排除，发现是将输入函数给劫持了

上为静态分析中的跳转地址，下为动调的跳转地址

动调跟进去发现一个新函数，直接去IDA里面找到这个位置

甚至没分析，p一下看看

由于劫持了整个接收输入的参数，而输入函数被调了两次，所以这边对两次都做了处理（16对应key，32对应flag，返回值为输入的内容，主打一个迷惑）

一个个看吧

首先是sub_E1046，里面用了个伪随机来对某个表进行了置换操作

AES的S盒

看来就是AES算法了，不过由于开始的S盒要先进行一个变换，直接动调搞出来整个S盒就行，在ret处下个断点

就可以在内存中找到了

之后提取一下逆S盒

def gen_inv_s_box():
    with open("./table.txt",'rb') as f:
        tmp = f.read()
        s_box_new = struct.unpack('i'*256,tmp)
    for i in range(len(s_box_new)):
        print(hex(s_box_new[i]),end=', ')
        if i % 16 ==0 and i !=0:
            print()
    print()
    print('#########################################')
    inv_s_box_new = [0] * 256
    # 生成逆 S-Box
    for i in range(256):
        inv_s_box_new[s_box_new[i]] = i
        # 输出逆 S-Box
    for i in range(len(inv_s_box_new)):
        print(hex(inv_s_box_new[i]),end=', ')
        if i % 16 ==0 and i !=0:
            print()

不过S盒和逆S盒丢进去直接解密不行（）

再次检查，发现shiftrows操作变了

AES中的shiftrows操作变成了invshiftrows，所以在解密的时候需要将invshiftrows操作换成shiftrows操作

还要注意密文长度，这边加密是分两组丢进去加密的，所以解密的时候要将密文对半开然后分别解密

上脚本

import struct
N_ROUNDS = 10

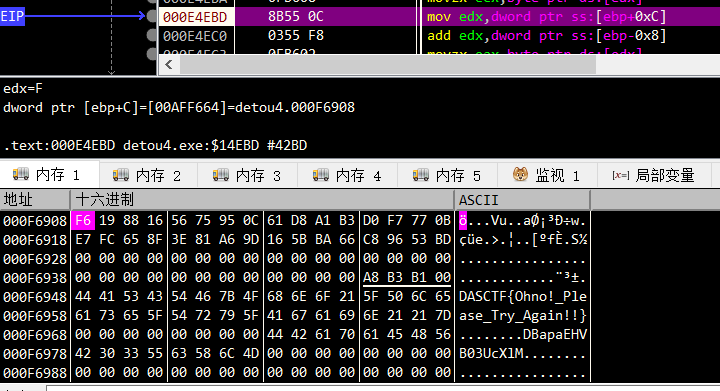
key = b'DBapaEHVB03UcXlM'
ciphertext = b'\x1f\xc1\xf4\xbe\xb7\x14u\x1d\xf9\x17\x19\xca\xc3r\x89\xd4\xbd\xc3\x8f_\xeb\x17\xa1.I\x932(a\x05\xc0\xa3'

s_box = (
    0x76, 0x4e, 0xda, 0x29, 0x9b, 0xbb, 0x74, 0xd6, 0xd0, 0xdc, 0xca, 0xfc, 0x39, 0x80, 0xed, 0x61, 0xa5, 
    0xc1, 0x6c, 0x79, 0xec, 0x5f, 0xb9, 0xa7, 0x42, 0x9a, 0xb, 0x75, 0xc9, 0xb4, 0xe8, 0x37, 0x78, 
    0x49, 0x10, 0x58, 0xae, 0x5b, 0xd, 0x8f, 0x7e, 0x45, 0x92, 0x4, 0x50, 0x3, 0xcf, 0x5e, 0x6e, 
    0x5, 0x6f, 0xa2, 0x52, 0xf, 0x38, 0xd7, 0x30, 0x28, 0x1c, 0x2d, 0x43, 0x51, 0x3e, 0x5a, 0x47, 
    0xfd, 0xa8, 0x22, 0x2, 0x9, 0x66, 0x6, 0xc0, 0x26, 0xe0, 0xb5, 0xe3, 0xd4, 0x99, 0x65, 0x77, 
    0xf0, 0xbd, 0x53, 0x3f, 0xdf, 0x83, 0x85, 0xde, 0x14, 0x5c, 0x9d, 0x4f, 0xfe, 0x98, 0xea, 0x94, 
    0xf2, 0x71, 0xa9, 0xad, 0x1f, 0x24, 0x11, 0xc7, 0x68, 0x33, 0x86, 0xa1, 0x6d, 0x9f, 0x84, 0xe4, 
    0x34, 0xc, 0x1a, 0x7b, 0xc3, 0xd1, 0x8d, 0x7a, 0x95, 0x93, 0xa4, 0x70, 0x8b, 0xaf, 0x60, 0x21, 
    0x7d, 0x2a, 0x73, 0xd9, 0x81, 0xb7, 0xef, 0xac, 0xa, 0x36, 0x35, 0x67, 0xf5, 0xcb, 0xf7, 0x25, 
    0x1e, 0xe7, 0x1b, 0xc5, 0x9c, 0x64, 0xe6, 0xc8, 0xa0, 0x40, 0xe1, 0x3d, 0xff, 0x4a, 0x63, 0xc4, 
    0x97, 0xd3, 0x69, 0x62, 0xa6, 0xd5, 0xf6, 0xaa, 0xfa, 0x7, 0xbe, 0x4c, 0xcc, 0xe, 0x96, 0xcd, 
    0xd2, 0xf4, 0xab, 0x17, 0xbc, 0x2e, 0xc2, 0x1, 0x82, 0x72, 0x8, 0xb6, 0x7c, 0xfb, 0x41, 0x3a, 
    0xb1, 0xf3, 0x2b, 0x6a, 0x1d, 0xee, 0xb3, 0xe5, 0x31, 0x4d, 0x89, 0x19, 0x87, 0x16, 0xe9, 0xd8, 
    0x5d, 0x8e, 0x13, 0x2f, 0x12, 0xb0, 0x44, 0x9e, 0x56, 0xdb, 0xbf, 0x57, 0x8c, 0x23, 0xb8, 0x0, 
    0x18, 0x3c, 0xf9, 0x90, 0xdd, 0xc6, 0x7f, 0x3b, 0x88, 0x55, 0x8a, 0x27, 0x2c, 0xb2, 0x59, 0xeb, 
    0x32, 0xa3, 0x48, 0x91, 0xce, 0xe2, 0x46, 0xf8, 0xba, 0x15, 0x20, 0x4b, 0x6b, 0x54, 0xf1,
)


inv_s_box = (
    0xe0, 0xb8, 0x44, 0x2d, 0x2b, 0x31, 0x47, 0xaa, 0xbb, 0x45, 0x89, 0x1a, 0x72, 0x26, 0xae, 0x35, 0x22, 
    0x67, 0xd5, 0xd3, 0x59, 0xfa, 0xce, 0xb4, 0xe1, 0xcc, 0x73, 0x93, 0x3a, 0xc5, 0x91, 0x65, 0xfb, 
    0x80, 0x43, 0xde, 0x66, 0x90, 0x49, 0xec, 0x39, 0x3, 0x82, 0xc3, 0xed, 0x3b, 0xb6, 0xd4, 0x38, 
    0xc9, 0xf1, 0x6a, 0x71, 0x8b, 0x8a, 0x1f, 0x36, 0xc, 0xc0, 0xe8, 0xe2, 0x9c, 0x3e, 0x54, 0x9a, 
    0xbf, 0x18, 0x3c, 0xd7, 0x29, 0xf7, 0x40, 0xf3, 0x21, 0x9e, 0xfc, 0xac, 0xca, 0x1, 0x5c, 0x2c, 
    0x3d, 0x34, 0x53, 0xfe, 0xea, 0xd9, 0xdc, 0x23, 0xef, 0x3f, 0x25, 0x5a, 0xd1, 0x2f, 0x15, 0x7f, 
    0xf, 0xa4, 0x9f, 0x96, 0x4f, 0x46, 0x8c, 0x69, 0xa3, 0xc4, 0xfd, 0x12, 0x6d, 0x30, 0x32, 0x7c, 
    0x62, 0xba, 0x83, 0x6, 0x1b, 0x0, 0x50, 0x20, 0x13, 0x78, 0x74, 0xbd, 0x81, 0x28, 0xe7, 0xd, 
    0x85, 0xb9, 0x56, 0x6f, 0x57, 0x6b, 0xcd, 0xe9, 0xcb, 0xeb, 0x7d, 0xdd, 0x77, 0xd2, 0x27, 0xe4, 
    0xf4, 0x2a, 0x7a, 0x60, 0x79, 0xaf, 0xa1, 0x5e, 0x4e, 0x19, 0x4, 0x95, 0x5b, 0xd8, 0x6e, 0x99, 
    0x6c, 0x33, 0xf2, 0x7b, 0x10, 0xa5, 0x17, 0x42, 0x63, 0xa8, 0xb3, 0x88, 0x64, 0x24, 0x7e, 0xd6, 
    0xc1, 0xee, 0xc7, 0x1d, 0x4b, 0xbc, 0x86, 0xdf, 0x16, 0xf9, 0x5, 0xb5, 0x52, 0xab, 0xdb, 0x48, 
    0x11, 0xb7, 0x75, 0xa0, 0x94, 0xe6, 0x68, 0x98, 0x1c, 0xa, 0x8e, 0xad, 0xb0, 0xf5, 0x2e, 0x8, 
    0x76, 0xb1, 0xa2, 0x4d, 0xa6, 0x7, 0x37, 0xd0, 0x84, 0x2, 0xda, 0x9, 0xe5, 0x58, 0x55, 0x4a, 
    0x9b, 0xf6, 0x4c, 0x70, 0xc8, 0x97, 0x92, 0x1e, 0xcf, 0x5f, 0xf0, 0x14, 0xe, 0xc6, 0x87, 0x51, 
    0xff, 0x61, 0xc2, 0xb2, 0x8d, 0xa7, 0x8f, 0xf8, 0xe3, 0xa9, 0xbe, 0xb, 0x41, 0x5d, 0x9d,
)


def shift_rows(s):
    '''
    s[0][0]   s[1][0]   s[2][0]   s[3][0]
    s[0][1]   s[1][1]   s[2][1]   s[3][1]
    s[0][2]   s[1][2]   s[2][2]   s[3][2]
    s[0][3]   s[1][3]   s[2][3]   s[3][3]
    '''
    s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]


def inv_shift_rows(s):
    '''
    s[0][0]   s[1][0]   s[2][0]   s[3][0]
    s[0][1]   s[1][1]   s[2][1]   s[3][1]
    s[0][2]   s[1][2]   s[2][2]   s[3][2]
    s[0][3]   s[1][3]   s[2][3]   s[3][3]
    '''
    s[1][1], s[2][1], s[3][1], s[0][1] = s[0][1], s[1][1], s[2][1], s[3][1]
    s[2][2], s[3][2], s[0][2], s[1][2] = s[0][2], s[1][2], s[2][2], s[3][2]
    s[3][3], s[0][3], s[1][3], s[2][3] = s[0][3], s[1][3], s[2][3], s[3][3]


def xtime(a): return (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)


def mix_single_column(a):
    # see Sec 4.1.2 in The Design of Rijndael
    t = a[0] ^ a[1] ^ a[2] ^ a[3]
    u = a[0]
    a[0] ^= t ^ xtime(a[0] ^ a[1])
    a[1] ^= t ^ xtime(a[1] ^ a[2])
    a[2] ^= t ^ xtime(a[2] ^ a[3])
    a[3] ^= t ^ xtime(a[3] ^ u)


def mix_columns(s):
    for i in range(4):
        mix_single_column(s[i])


def inv_mix_columns(s):
    # see Sec 4.1.3 in The Design of Rijndael
    for i in range(4):
        u = xtime(xtime(s[i][0] ^ s[i][2]))
        v = xtime(xtime(s[i][1] ^ s[i][3]))
        s[i][0] ^= u
        s[i][1] ^= v
        s[i][2] ^= u
        s[i][3] ^= v

    mix_columns(s)


def bytes2matrix(text):
    """ Converts a 16-byte array into a 4x4 matrix.  """
    return [list(text[i:i+4]) for i in range(0, len(text), 4)]


def matrix2bytes(m):
    return bytes(sum(m, []))


def add_round_key(s, k):
    for i in range(4):
        for j in range(4):
            s[i][j] ^= k[i][j]


def inv_sub(s):
    for i in range(4):
        for j in range(4):
            s[i][j] = inv_s_box[s[i][j]]


def expand_key(master_key):
    """
    Expands and returns a list of key matrices for the given master_key.
    """
    # Round constants https://en.wikipedia.org/wiki/AES_key_schedule#Round_constants
    r_con = (
        0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,
        0x80, 0x1B, 0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A,
        0x2F, 0x5E, 0xBC, 0x63, 0xC6, 0x97, 0x35, 0x6A,
        0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5, 0x91, 0x39,
    )
    # Initialize round keys with raw key material.
    key_columns = bytes2matrix(master_key)
    iteration_size = len(master_key) // 4
    # Each iteration has exactly as many columns as the key material.
    columns_per_iteration = len(key_columns)
    i = 1
    while len(key_columns) < (N_ROUNDS + 1) * 4:
        # Copy previous word.
        word = list(key_columns[-1])

        # Perform schedule_core once every "row".
        if len(key_columns) % iteration_size == 0:
            # Circular shift.
            word.append(word.pop(0))
            # Map to S-BOX.
            word = [s_box[b] for b in word]
            # XOR with first byte of R-CON, since the others bytes of R-CON are 0.
            word[0] ^= r_con[i]
            i += 1
        elif len(master_key) == 32 and len(key_columns) % iteration_size == 4:
            # Run word through S-box in the fourth iteration when using a
            # 256-bit key.
            word = [s_box[b] for b in word]

        # XOR with equivalent word from previous iteration.
        word = bytes(i ^ j for i, j in zip(word, key_columns[-iteration_size]))
        key_columns.append(word)

    # Group key words in 4x4 byte matrices.
    return [key_columns[4*i: 4*(i+1)] for i in range(len(key_columns) // 4)]




def decrypt(key, ciphertext):
    round_keys = expand_key(key)  # Remember to start from the last round key and work backwards through them when decrypting
    # Convert ciphertext to state matrix
    Cipher_matrix = bytes2matrix(ciphertext)
    # Initial add round key step
    add_round_key(Cipher_matrix, round_keys[-1])
    for i in range(N_ROUNDS - 1, 0, -1):
        shift_rows(Cipher_matrix)
        inv_sub(Cipher_matrix)
        add_round_key(Cipher_matrix, round_keys[i])
        inv_mix_columns(Cipher_matrix)
    # Run final round (skips the InvMixColumns step)
    shift_rows(Cipher_matrix)
    inv_sub(Cipher_matrix)
    add_round_key(Cipher_matrix, round_keys[0])

    # Convert state matrix to plaintext
    plaintext = matrix2bytes(Cipher_matrix)
    return plaintext


print(key.hex(), ciphertext.hex())
print(decrypt(key, ciphertext[:16]))
print(decrypt(key, ciphertext[16:]))

# b'DASCTF{D3t0urs_H'
# b'oOk_Functions!!}'
# DASCTF{D3t0urs_HoOk_Functions!!}